“I am able to prove that not only light, colour, and the like, but also movement, shape, and space are all nothing but apparent qualities” 

LEIBNIZ

“I only use numbers because it is a way of writing without describing”

HANNE DARBOVEN

NUMBERS.

Sensual and optical realities both hide a common question: their apparent solidity. What represents the concrete character of sight, of feeling, of smell, when compared with the logical process with which we qualify our quantitative presence in the world? Every process is enumerable. Numbers are that necessary instrument for defining a thought which processes the Infinite. In order to accept a mathematical description of nature, physicists were forced to abandon the common world of experience, the world of the perception of the senses. To understand the meaning of this abandonment, we must go beyond that fragile boundary that divides physics from mathematics. Art, whenever it has to do with numbers, when it flaunts its structural version, can be the mobile threshold through which we link quality and quantity by way of the iconic value of numbers. The number takes on the part of the main character with the Avantgardes. It enters into the picture, into the painting itself, into the collage, into the installation, it enters into the system of exchange and hardens as irreplaceable thought in order to understand the speed and progress of chance. As in the comparison between physics and mathematics, art has posed queries able to understand the relationships between observer and reality, between subject and object, in other words it has placed those questions – that have tormented philosophers since the dawn of reason, since the original cyphers were still immersed in the nebula of original experience – onto a visual level.

1. Euclid and Fibonacci: numeral space

Euclidean space is an axiomatic one. His own form of geometry which is based on certain commonly-shared notions that are accepted as postulates, has produced elementary theorems, upon which even today we base minimalist, rationalistic, naturalistic thought: the ‘correct way of thinking’ (which he calls the rules of inference), are posed as if provided by propositions whose truth is accepted without any demonstration. The propositions (the axioms) act as starting-point from where we rigorously demonstrate (using the rules of inference) all that follows (the theorems).

2. Artists, engineers and architects:
Leonardo da Vinci and Piero della Francesca.

Leonardo da Vinci noted that the numbers of Fibonacci matched the position of leaves upon different types of plant, or rather phyllotaxis. That progression corresponded to the golden proportion. The French painter, Seurat, made conscious use of it in many of his works. Use of the numbers of Fibonacci are to be seen in the “fugues” of Johannes Sebastian Bach, in the Sonata in A D959 by Schubert, in some of the works of Debussy and Ravel, in the Allegro Barbaro of Béla Bartók.

ALIGHIERO BOETTI

3. Game and chaos in the case of Dada

Every puzzle is a question of putting things together. If a single piece is missing, the whole system goes mad. A child’s room is in a state of chaotic orderliness which he elaborates by adding chaos to chaos. Jean Arp let shapes fall on to a surface and studied their relationships.

GINO DE DOMINICIS

4. Numbers and letters: surrealist science
                                              

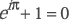
The formula of Euler, a great Swiss mathematician of the 18th century, establishes an apparently amazing relationship between certain constants of universal usage: at first sight it would seem indeed very strange that (a transcendent number raised to the imaginary unit and multiplied by another transcendent number) could be equal to –1. It is precisely in this transcendent relation that that equation permits the greatest paradox.

5. Florensky and De Chirico: the experience of the sacred and of the enigma

The metaphysical experience brings about infinite unity. Numbers signal the interpretations of the symbol. The number One mirrors itself and in such a way, coming back to itself, comes true like a new One, which is Two and so gradually becomes all the successive numbers. Just like in the obsessive repetitions of Warhol, repetition produces a harmony which frees the shape from the contents.