“Io sono capace di provare che non solo la luce, il colore, e cose simili,

ma anche il moto, la forma e lo spazio non sono altro che qualità apparenti” 

LEIBNIZ

“I only use numbers because it is a way of writing without describing”

HANNE DARBOVEN

NUMERI.

La realtà sensuale e la realtà ottica nascondono un comune problema: la loro concretezza apparente. Qual é la concretezza del vedere, del sentire, dell'odorare, paragonata al processo logico con cui qualifichiamo la nostra presenza quantitativa nel mondo? Ogni processo è enumerabile. I numeri sono quello strumento necessario a definire un pensiero che elabori l'Infinito. Nell'accettare una descrizione matematica della natura, i fisici sono stati obbligati ad abbandonare il mondo comune dell'esperienza, il mondo della percezione dei sensi. Per comprendere il significato di questo abbandono, è necessario oltrepassare la fragile frontiera che divide la fisica dalla matematica.
L'arte, quando si interessa dei numeri, quando ostenta la sua versione strutturale, può essere la soglia mobile attraverso cui far combaciare qualità e quantità attraverso il valore iconico dei numeri. Il numero assume un protagonismo con le Avanguardie.
Entra nel quadro, entra nel lavoro della pittura, del collage, dell'installazione, entra nel sistema degli scambi e si sedimenta come pensiero insostituibile per capire la velocità e le progressioni del caso. Come nel confronto tra fisica e matematica, l'arte ha posto dei quesiti comprendenti e relazioni fra l'osservatore e la realtà, fra soggetto ed oggetto, in altre parole ha posto su un piano visivo quelle domande che hanno assillato i filosofi fin dall'alba della ragione, fin dai primi numeri ancora immersi nella nebulosa dell'esperienza originaria.

1. Euclide e Fibonacci: lo spazio numerale

Lo spazio euclideo è uno spazio assiomatico. La sua geometria basata su alcune nozioni comuni, accettate come postulati, ha prodotto dei teoremi elementari, su cui si costruisce ancora oggi il pensiero minimale, razionale, naturalista: il 'corretto modo di ragionare' (che lui chiama le regole di inferenza), si pongono come date delle proposizioni la cui verità viene accettata senza dimostrazione. Le proposizioni (gli assiomi) servono come punto di partenza dal quale dimostrare in modo rigoroso (usando le regole di inferenza) tutto quanto segue (i teoremi).

2. Artisti, ingegneri e architetti:
Leonardo da Vinci e Piero della Francesca

Leonardo da Vinci si accorse che i numeri di Fibonacci tornavano nella posizione delle foglie sui diversi tipi di piante, ovvero nella fillotassi. Quella progressione corrispondeva alla proporzione aurea. Il pittore francese Seurat ne ha fatto un uso consapevole in molte delle sue opere. Esempi dell'uso dei numeri di Fibonacci si hanno nelle "fughe" di Johannes Sebastian Bach, nella Sonata in la D 959 di Schubert, in parte delle opere di Debussy e di Ravel, nell’Allegro Barbaro di Béla Bartók.

ALIGHIERO BOETTI

3. Il gioco e il caos nel caso Dada

Ogni puzzle è un componimento. Se manca un pezzo impazzisce il sistema. La stanza di un bambino è un ordine caotico che egli rielabora aggiungendo nuovo caos al caos. Jean Arp lasciava cadere le forme su una superficie e ne studiava la relazione.

GINO DE DOMINICIS

4. Numeri e lettere: la scienza surrealista
                                              

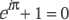
Questa formula di Eulero, grande matematico svizzero del XVIII secolo, stabilisce una relazione apparentemente strabiliante tra alcune costanti di utilizzo universale: a prima vista sembra davvero molto strano che (un numero trascendente elevato all'unità immaginaria moltiplicata per un altro numero trascendente) possa essere uguale a -1. É proprio in questa relazione trascendente che quella equazione consente il più grande paradosso.

5. Florenskij e De Chirico: l'esperienza del sacro e dell'enigma

L'esperienza metafisica attua l'infinita unità. I numeri segnano le interpretazioni del simbolo. L'uno si rispecchia e in tal modo, tornando su se stesso, s'invera come nuovo Uno, che è due e così diventa via via tutti i numeri successivi. Come nelle iterazioni ossessive di Warhol, la ripetizione produce un'estetica che libera la forma dal contenuto.